Over Under 13 Blackjack Odds
Both the Over 13 and Under 13 bets lose on a total of 13. Wins on both bets pay even money. The Majestic casino in Panama City offers a bet on a total of exactly 13, which pays 10 to 1. Over-13 bets should be placed when the count is +3 and above. Under-13 bets should be placed when the count is -4 and below. When playing Over/Under blackjack with this counting scheme, virtually all of the player's profit comes from the over-13 and under-13 side bets.
- Over Under 13 Blackjack Odds Card Game
- Over Under 13 Blackjack Odds Poker
- Over Under 13 Blackjack Odds Against
- Over Under 13 Blackjack Odds Explained
The Over/Under Report:
A System for Beating
the Over/Under Side Bet
By Arnold Snyder
© 1989 Arnold Snyder Introduction
Much of this report will seem too technical for the average player. If you don’t quite grasp some of the mathematical concepts, don’t worry about it. The over/under card counting system described is simple and easy to apply. Just follow the recommendations and you should have no trouble. The more technical explanations are for the math-heads who will hopefully appreciate the full story. –A.S.
The Over/Under Rule
At the time of this writing (August, 1989) the only U.S. casino that offers the over/under rule at its blackjack tables is Caesars Tahoe in Stateline, Nevada. [Editor's note: As of 2006, the Over/Under rule is not offered in the U.S. However, it is offered in casinos in Eastern Europe, Asia, and elsewhere.] Caesars has a two-year exclusive contract with the developer of this rule variation to offer this game in the U.S. In the summer of 1990, the developer may market this rule variation to other U.S. casinos.

Note: Technically, the “rule” of a game cannot be protected by copyright or patent. However, the over/under bet requires an alteration of the blackjack table layout in order to facilitate the side bet. The developer, Mr. Ken Perrie, a Caesars’ pit boss, owns the rights to the design of his unique table layout.
Bets on the regular blackjack hand are placed in the large central circle (the normal betting spot). Optional over/under side bets may be placed in the small circles to the left and right of the center circle. The side bet circles will be labelled 'over' and 'under.'
How the Over/Under Bet Works
As with the normal blackjack bet, over/under bets must be placed prior to the deal. Over/under bets are always optional side-bets. No player at an over/under game is ever required to place an over/under bet.
The player who places a bet in the over circle is betting that his first two cards will total more than 13. The player who places a bet in the under circle is betting that his first two cards will total less than 13. These are even money bets. Aces always count as one when determining totals for the over/under bet. King, Queen, Jack and 10 all count as ten. All other denominations count as their face values.
Over/Under Restrictions
No player may place an over/under bet unless he is betting on a regular blackjack hand. The amount bet on over or under may never exceed the amount bet on the blackjack hand. At Caesars Tahoe at this time, no over or under bet may ever exceed $100.
All over/under bets are settled prior to the play of the blackjack hands. The outcome of over/under bets have no effect on any aspect of the blackjack game.
Analysis of the Over/Under Game
Compared to regular blackjack, the over/under game is easy to analyze. By considering all possible two-card totals, it is a straightforward calculation to count how many of these hands total over 13, and how many total under 13.
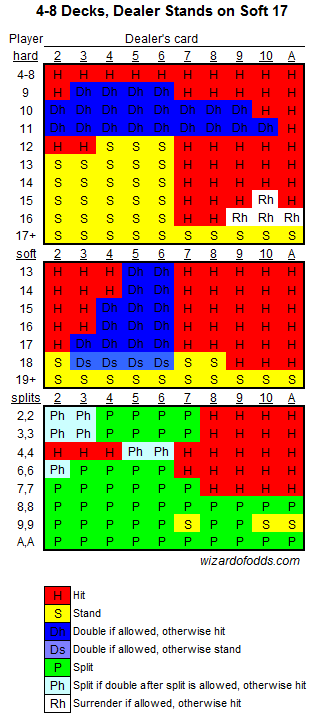
If we assume that the player will bet one unit on every hand that his hand will total over 13, then compare the results of his wins and losses, we see that he will lose about 6 1/2% of his total amount bet. If he always bets on the under side, he will lose slightly more than 10% of his total under bets. The house obtains its advantage from the fact that the house always wins over and under bets on player totals of exactly 13.
So, “basic strategy” for the over/under bets is to never bet on either side. The house has the advantage either way in the long run.
However, it is also obvious that this house advantage will change throughout the course of the game. An excess of high cards remaining to be dealt would make a hand totaling over 13 more probable. And an excess of low cards will make an under 13 hand more probable.
In order to devise an optimal card counting system that will tell us when the over or under bets have become advantageous, we must first figure out the effects of removing each of the individual cards. Again, this is a very straightforward mathematical calculation. It is done exactly like the initial calculation we did to determine the house advantage off the top of the six-deck shoe [editor's note: analysis of 1, 2, 4 and 8 deck Over/Under games is included in the supplement at the end of this report], except that we remove one of each denomination of card in turn, refiguring the outcome on the over and under bets.
We will find, for instance, that when we remove one ten-valued card, we come up with slightly fewer possible two-card hands that will total over 13, and slightly more two-card hands that will total under 13. The difference between the house advantage off the top and minus one ten tells us the effect of removing a ten. Note that each card will have two effects of removal—one effect on the over bet, and a different effect on the under bet.
These are the approximate effects of removal in percent for each denomination of card in the 6-deck over/under game (for effects of removal in 1, 2, 4, and 8-deck games, see the supplement at the end of this report):

| A | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Over: | +0.60 | +0.60 | +0.60 | +0.20 | +0.11 | +0.01 | -0.09 | -0.19 | -0.29 | -0.39 |
| Under: | -0.71 | -0.71 | -0.31 | -0.21 | -0.11 | -0.01 | +0.08 | +0.18 | +0.28 | +0.38 |
These effects are much greater than those for regular blackjack. The removal of one ace, for instance, in a 6-deck blackjack game, has an effect of approximately -0.10% on your regular blackjack hand. Removing an ace has 6 times this effect on any over bet, and seven times this effect on an under bet.
It is easy to see why the ace and deuce, for instance, have such high effects of removal. Consider that if either one of your cards is an ace or a deuce, you could not possibly lose the under bet, nor could you possibly win the over bet.
Also note that these effects of removal are for removing just one card from the top of a 6-deck shoe. In regular blackjack, effects of removal are usually given for removing one card from the top of a single deck. The effect of removing an ace from a single deck is approximately -0.6% on your regular blackjack hand. If the over/under bet were allowed in a single-deck game [editor's note: 1, 2, 4 and 8-deck games with the Over/Under rule later became available], the effects of removing one ace would be -4.40% on the under bet, and +3.73% on the over bet.
In other words, even though the house advantage over you on the over bet in a single-deck game is about 6.8%, the removal of just one ace and one deuce in a single-deck over/under game would put the edge in your favor by almost 0.7%! Although there are no single-deck over/under games at this time, the volatile swings in advantage caused by the effects of removal make even the 6-deck game a profitable game for card counters. Removal of a single ace, deuce, or three, for instance, from the 6-deck shoe has more effect on your over/under betting opportunities than the removal of any of these cards would in a single-deck regular blackjack game.
Devising an Over/Under Card Counting System
First let’s look at how well some common blackjack card counting systems correlate to the over/under bet:
Correlation of Various Card Counting Systems to the Over/Under Bet
| COUNT SYSTEM | A | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | UND | OVR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EINSTEIN/HI OPT I | ||||||||||||
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | -1 | -0.56 | 0.64 | |
| DHM/GORDON | ||||||||||||
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | -1 | -0.74 | 0.79 | |
| GRIFFIN-1 | ||||||||||||
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | -1 | -0.46 | 0.46 | |
| BRAUN +-/DUBNER/HI-LO | ||||||||||||
| -1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | -1 | -0.50 | 0.57 | |
| USTON +- | ||||||||||||
| -1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | -1 | -0.32 | 0.41 | |
| REVERE ADVANCED +- | ||||||||||||
| 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | -1 | -1 | -0.73 | 0.78 | |
| CANFIELD EXPERT | ||||||||||||
| 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | -1 | -1 | -0.55 | 0.62 | |
| ITA GREEN FOUNTAIN | ||||||||||||
| -1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | -1 | -1 | -0.50 | 0.56 | |
| HI OPT II/STEPPINE | ||||||||||||
| 0 | 1 | 1 | 2 | 2 | 1 | 1 | 0 | 0 | -2 | -0.64 | 0.67 | |
| ANDERSON/REPPERT | ||||||||||||
| -2 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | -1 | -1 | -0.30 | 0.38 | |
| R&T POINT COUNT | ||||||||||||
| 0 | 1 | 1 | 2 | 2 | 2 | 0 | 0 | 0 | -2 | -0.63 | 0.66 | |
| REVERE POINT COUNT | ||||||||||||
| -2 | 1 | 2 | 2 | 2 | 2 | 1 | 0 | 0 | -2 | -0.42 | 0.50 | |
| CANFIELD MASTER/GRIFFIN-2 | ||||||||||||
| 0 | 1 | 1 | 2 | 2 | 2 | 1 | 0 | -1 | -2 | -0.64 | 0.66 | |
| WONG'S HALVES | ||||||||||||
| -1 | 0.5 | 1 | 1 | 1.5 | 1 | 0.5 | 0 | -0.5 | -1 | -0.44 | 0.51 | |
| GRIFFIN-3/USTON ADVANCED | ||||||||||||
| 0 | 1 | 2 | 2 | 3 | 2 | 2 | 1 | -1 | -3 | -0.61 | 0.65 | |
| REVERE ADVANCED ('71) | ||||||||||||
| -4 | 2 | 3 | 3 | 4 | 3 | 2 | 0 | -1 | -3 | -0.38 | 0.46 | |
| REVERE ADVANCED ('74) | ||||||||||||
| 0 | 2 | 2 | 3 | 4 | 2 | 1 | 0 | -2 | -3 | -0.68 | 0.71 | |
| ZEN | ||||||||||||
| -1 | 1 | 1 | 2 | 2 | 2 | 1 | 0 | 0 | -2 | -0.51 | 0.55 | |
Note that the most common counting systems correlate poorly. Hi-Opt I has about a 64% correlation on the over bet, and about 56% on the under bet. The High-Low is worse; 57% over and 50% under. The Zen Count’s about the same. The Uston +/- is terrible. The best normal card counting system for this game is the DHM (a mail order card counting system of years gone by, no longer in print.) Second best is the Revere Advanced +/-, another ancient system no longer in wide usage. Third best is the 1974 Revere Advanced Point Count, which correlates 71% on the over bet and 68% on the under bet. But this is another system that is not widely available, and a difficult level 4 strategy that would be unwieldy for most players.
Considering the fact that the effects of removal indicate to us that over/under betting opportunities provide far more profit potential in this 6-deck game than regular blackjack, let’s devise some card counting systems specifically aimed at attacking the over/under. Here are six possible over/under counts:
| COUNT | A | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | UND | OVR |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Count 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | -0.90 | 0.92 |
| Count 2 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | -1 | -1 | -0.89 | 0.91 |
| Count 3 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | -1 | -1 | -1 | -0.86 | 0.88 |
| Count 4 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | -1 | -1 | -1 | -0.94 | 0.97 |
| Count 5 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | -1 | -1 | -1 | -0.98 | 0.96 |
| Count 6 | 2 | 2 | 2 | 1 | 1 | 0 | 0 | 0 | 0 | -2 | -0.91 | 0.94 |
We can see here that Count #4 and Count #5, both level two systems, correlate the best. My choice of system, however, is Count #1, for a number of reasons. First of all, as a level 1 system, it’s the easiest to learn and use. Second, if I assume that your are going to be using your over/under count not only to make over/under betting decisions, but also to play your regular blackjack hand, Count #1 is the best all-purpose card counting system. It has an insurance efficiency of 85%, the same as Hi-Opt I, and a playing efficiency of 47%, not that much worse than the High-Low’s 51%. For convenience, let’s call Count #1 the “Over/Under Count.”
The Over/Under Count
| A | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | UND | OVR | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| The Over/Under Count | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | -1 | -0.90 | 0.92 |
Although it is possible to develop many multi-parameter approaches that would optimize potential profits on both the over/under bets and the regular blackjack hand, I would not consider these more difficult strategies to be worth the trouble. Having a system with a high betting correlation for your regular blackjack hand is useless. The over/under bets are much more important. And to strive for a playing efficiency of 60%, or even 70%, in a 6-deck game, is a waste of time. The potential strategy gains are extremely small.
The vast majority of your profit potential will come from betting accurately on your over/under opportunities. You only want to be and play the regular blackjack hand well enough to reduce the ½% house advantage to as near a break even point as possible. You can’t table hop over/under games. You’re likely to miss betting opportunities on the under side when the count is negative.
For extreme ease, if you are already using a balanced level 1 card counting system, such as Hi-Opt I or the Hi-Lo count, you could use the same strategy tables to play your hand using the Over/Under Count, and you will be playing your regular blackjack hand with great accuracy. This is a count-per-deck strategy chart drawn up specifically for using the Over/Under Count to play your blackjack hands.
Count Per Deck Strategy Chart for the Over/Under Count
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | A | |
|---|---|---|---|---|---|---|---|---|---|---|
| 16 | +5 | +3 | 0 | +3 | ||||||
| 15 | +5 | |||||||||
| 14 | -4 | |||||||||
| 13 | 0 | -2 | -3 | -4 | ||||||
| 12 | +4 | +2 | +1 | -1 | -2 | |||||
| A7 | +5 | 0 | ||||||||
| 11 | -4 | -4 | -1 | |||||||
| 10 | -5 | -2 | +3 | |||||||
| 9 | +1 | -1 | -4 | +4 | ||||||
| 8 | +4 | +2 | ||||||||
| Insurance: +3 | ||||||||||
The next step in analyzing this game is to figure out the value of each point-per-deck; in other words, how much does your (dis)advantage change with each true count? The value of a point is a function of the effects o9f removal and the assigned point values. Since we have different effects of removal for the over bet, the under bet, and the regular blackjack hand, each true count will technically have three different values.
If you have a background in statistics, you may calculate the value of a true point for each of the three possible bets by dividing the inner products of the effects of removal and their respective assigned point values by the sum of the squares of the point values. Note that you should first multiply the 6-deck effects of removal for the over and under bets by 6, in order to obtain the effects of removal per deck. The effects of removal for the regular blackjack hand are in Peter Griffin’s Theory of Blackjack, as well as numerous other publications. Griffin also explains how to find the inner product.
Fortunately, Sam Case has a computer program that spits out this data in a fraction of a second. You don’t have to do the math, or even understand it. Just trust me that each true count using the Over/Under Count described above has the following values:
| Over bet: | 2.70% |
| Under bet: | 2.58% |
| Regular blackjack hand: | 0.35% |
Do note that each true count with this system affects your regular blackjack advantage by only -.35%, instead of the 0.5% we usually expect with level one systems. This is due to the lower betting correlation, caused primarily by assigning a plus value to the ace. We are willing to relinquish the betting accuracy on our blackjack hand since the over/under bets offer so much more profit potential.
Caesars Tahoe’s 6-deck games use downtown Vegas rules with double after splits. The player’s starting advantage in this game is -0.54%. The following chart shows your expectation in percent on each of the three possible bets you may make at various true counts.
6-Deck Expectation for Various True Counts
| True Count | Blackjack Bet | Over Bet | Under Bet |
|---|---|---|---|
| -9 | -3.69 | -30.85 | +13.15 |
| -8 | -3.34 | -28.15 | +10.57 |
| -7 | -2.99 | -25.45 | +7.99 |
| -6 | -2.64 | -22.75 | +5.41 |
| -5 | -2.29 | -20.05 | +2.83 |
| -4 | -1.94 | -17.35 | +0.25 |
| -3 | -1.59 | -14.65 | -2.33 |
| -2 | -1.24 | -11.95 | -4.91 |
| -1 | -0.89 | -9.25 | -7.49 |
| 0 | -0.54 | -6.55 | -10.07 |
| +1 | -0.19 | -3.85 | -12.65 |
| +2 | +0.16 | -1.15 | -15.23 |
| +3 | +0.51 | +1.55 | -17.81 |
| +4 | +0.86 | +4.25 | -20.39 |
| +5 | +1.21 | +6.95 | -22.97 |
| +6 | +1.56 | +9.65 | -25.55 |
| +7 | +1.91 | +12.35 | -28.13 |
| +8 | +2.26 | +15.05 | -30.71 |
| +9 | +2.61 | +17.75 | -33.39 |
Now, we’re ready to devise a strategy for attacking this game. One of the nice features about the over/under bets is that you never have to place them. This means that all of the negative advantages that occur on these bets at various counts will have no effect on your expectation since you will not be betting. So, let’s simplify the above chart to show the effective player/house advantages at each true count, assuming that the player only bets on over or under when the player has the edge.
It can also be shown that if we place two equal simultaneous bets on events with different expectations, our combined expectation is the same as if we had placed one bet of the total amount on the average of the two expectations. For instance, the expectation on your blackjack hand at a true count of +3 is +0.51%. The expectation on the over bet is +1.55%. Therefore, if I place a $100 bet on each of these, I would expect to profit in the long run 51 cents on my blackjack hand and $1.55 on the over bet. This is a total profit of $2.06 on the $200 of total action. $2.06 is 1.03% of $200. 1.03% is also the average of .51% and 1.55%.
This means that we can further simplify the chart of our expectations at various true counts by averaging our advantages when we place simultaneous bets. The following simplified chart shows your actual expectations at various true counts when you place over or under bets when you have the advantage.
Expectation at Various Over/Under Count True Counts with the Over/Under Bet
| Count | % Expectation |
|---|---|
| -9 | +4.73* |
| -8 | +3.62* |
| -7 | +2.50* |
| -6 | +1.39* |
| -5 | +0.27* |
| -4 | -0.85* |
| -3 | -1.59 |
| -2 | -1.24 |
| -1 | -0.89 |
| 0 | -0.54 |
| +1 | -0.19 |
| +2 | +0.16 |
| +3 | +1.03* |
| +4 | +2.56* |
| +5 | +4.08* |
| +6 | +5.61* |
| +7 | +7.13* |
| +8 | +8.65* |
| +9 | +10.18* |
| * Combined blackjack and over/under bets | |
Now you can see why this is such a nice game for card counters. Not only does your advantage go up on both positive and negative counts—and quite a bit higher than a card counter’s advantage every rises—but the house never has an advantage over you of much more than 1 ½%.
We can now analyze your profit potential in this game using standard 6-deck frequency distributions. The frequency distributions for this count are identical to those for the Hi-Opt I counting system.
I visited Caesars Tahoe in June of 1989, and again in August, in order to play the over/under games and observe the shuffling standards. There is a wide variance in deck penetration on Caesars’ 6-deck games. On an average, most dealers deal out about 4 ½ decks, or 75% between shuffles. During both of my visits, however, I was able to find dealers who dealt out 5 decks. You will also see dealers who do not deal out much more than 4 decks.
As with any blackjack game, deep penetration is important for card counters. These are frequency distributions, in hands-per-hundred for the Over/Under Count, assuming 4 decks dealt out, 4 ½ decks dealt out, and 5 decks dealt out.
| True Count | 4 Decks Dealt | 4.5 Decks Dealt | 5 Decks Dealt |
|---|---|---|---|
| -9 | 0 | 0 | 0.5 |
| -8 | 0 | 0.5 | 0.5 |
| -7 | 0.5 | 0.5 | 1 |
| -6 | 0.5 | 1 | 1.5 |
| -5 | 1 | 1 | 1.5 |
| -4 | 2 | 2 | 2.5 |
| -3 | 3 | 3.5 | 4 |
| -2 | 8 | 7.5 | 7 |
| -1 | 14 | 14 | 13 |
| 0 | 42 | 40 | 37 |
| +1 | 14 | 14 | 13 |
| +2 | 8 | 7.5 | 7 |
| +3 | 3 | 3.5 | 4 |
| +4 | 2 | 2 | 2.5 |
| +5 | 1 | 1 | 1.5 |
| +6 | 0.5 | 1 | 1.5 |
| +7 | 0.5 | 0.5 | 1 |
| +8 | 0 | 0.5 | 0.5 |
| +9 | 0 | 0 | 0.5 |
If you are mathematically inclined, you may use these frequency distributions to estimate your potential advantage and win rate in dollars with various betting approaches. My analysis yields the following data.
Flat Betting
For the over/under game, we’ll define flat betting as placing the same size bet on all of your blackjack hands, but also placing a bet of the same amount on either the over or under only when it is advantageous to do so. Using the Over/Under Count, this means placing an over bet when your true count is +3 or more, and placing an under bet when your true count is -4 or less.
Flat betting is not a good approach to this game, though it is moderately favorable when the penetration is deep. If only 4 decks are being dealt out, your expectation is -0.1%. If 4 ½ decks are dealt out, your expectation is 0.1%.
In other words, with normal penetration, you will be playing a break even game. If 5 decks are dealt out, your expectation goes up to +0.4%. With $100 bets, and 100 hands per hour, this would be a potential win rate of about $50 per hour. If you have a large bankroll and you can afford the potential fluctuation, this approach may appeal to you—especially if you’re playing for comps. Generally, I do not advise serious players to risk so much for so little. It is remarkable that you are able to get any advantage at all flat-betting a 6-deck game, playing through all negative counts.
1-to-2 Spread
You bet one unit on your blackjack hand when the true count is between -5 and +2. Below -5, or above +2, you bet 2 units. At -4 or below, you match your blackjack bet with an under bet. This means you will be betting one unit on under at -4 and -5, and two units on the under at -6 or below. At +3 or above, you match your two unit blackjack bet with a 2 unit over bet.
With 4 decks dealt out, your expectation is +0.2%, nothing to write home about. With 4 ½ decks dealt out, you’ll expect to win at the rate of about 0.5%. With 5 decks dealt out, you’ll have a full 1% expectation. Spreading from $50 to $100, this would make you about $75 per hundred hands.
1-to-4 Spread
Over Under 13 Blackjack Odds Card Game
I analyzed this spread with a 1 unit bet on the blackjack hand from -4 to +1; 2 unit blackjack bets at -5 and +2; 4 unit blackjack bets below -5 and above +2. Under bets match the blackjack bets (1, 2 or 4 units) at -4 and below. Over bets match the blackjack bets (4 units only) at +3 and above.
With 4 decks dealt out, this spread will get you an advantage of about 0.7%, not bad for the poor shuffle point. 4 ½ decks dealt out will get you a 1.1% advantage. And with 5 decks dealt out, your expectation is about 1.6%, or about $88 per hundred hands.
You may have noticed that the percentage advantage seems to be climbing with larger spreads faster than the $ expectation. For instance, flat-betting $100 chips with 5 decks out provides a 0.4% advantage, and about $50/hour. Using a 1-to-4 spread, your advantage climbs to 1.6%, but $ expectation is only $88/hour.
The reason for this is that we are obtaining the larger spread by lowering the minimum bet, as opposed to raising the maximum. Since the maximum bet allowed is $100, I’m analyzing the maximum potential dollar return for players who can afford it. Smaller stakes players would find that their $ win rate advanced as expected if they raised their top bets. For instance, flat betting $25 chips, with 5 decks dealt out, would net about $12 per hour. Spreading from $25 to $50 would get you about $38 per hour. And spreading from $25 to $100 would take in about $88 per hour.
I’m analyzing this game with conservative spreads so that you can see that it is not difficult to get the best of this 6-deck game, even with a small spread. Remember, if you’re barred at Caesars Tahoe, there are no other casinos in this country that offer over/under games at this time. Brave fools who either have, or believe they have, incredible acts, may use the frequency distributions provided to discover that they will have no trouble killing the game, even with only 4 decks dealt, with a spread of $5 to $100. Good luck!
Players with substantial bankrolls, who are put off by the limitations of the $100 max bet, may be tempted to analyze the potential win rates if you spread to multiple hands when the over/under bets are favorable. Such tactics will greatly increase your expectation. If you are spreading from $25 to $100 on one hand, using the 1-to-4 strategy described above, and playing a second hand only when the true count is at +3 and above, or -6 and below, your expectation would be about 2.2%, and about $190/hour.
Over/Under Count Bankroll Requirements
One of the nice things about the over/under bet is that it is a true side bet. Betting $100 each on your blackjack hand and the over bet, simultaneously, is not the same thing, as far as fluctuations go, as betting $200 on your blackjack hand, or even playing two simultaneous blackjack hands. The reason for this is that the over/under bets are not affected by the dealer’s upcards.
When you are playing simultaneous blackjack hands, you must account for the covariance. In other words, if the dealer gets a total of 20, both of your hands are going up against this strong total. If the dealer gets a natural, neither of your hands win money. But over/under bets are not tied to the dealer’s hand in any way. If you place an over bet, and you are dealt a total of 14, you win regardless of what the dealer has.
In fact, one of the first things you will notice when playing this game is how the over bet, especially, acts as a hedge against most of your losing stiffs when you have a big bet out. Much of the pain of being dealt a 14, 15 or 16 vs. a dealer 10, when you’ve got a big bet on the table, is eased by collecting on the over bet prior to having to play your miserable stiff.
Another nice feature of the over/under bets is that your advantage climbs so dramatically with each true count. A blackjack player whose moderate bankroll would never allow bets above $25 would not infrequently be able to place $100 over/under bets, because his combined blackjack and over/under advantage will be 4% or more. This is virtually unheard of in any “normal” 6-deck game.
For this reason, even if you can’t afford to spread from 1-to-4 according to the strategy I’ve outlined, with your 4 unit bet placed at +3 or above, you may be able to use this spread if you wait for higher advantages for your big bet. At +3, your combined advantage is about 1%; at +4, it’s about 2 ½%; at +5, it’s more than 4%! If you get into the deeply dealt games, you will see opportunities like this regularly.
General guidelines: With a very small bankroll—say $1000—plan on spreading from $5 to $10 for most of your play according to the betting guidelines above. But look for deeply dealt games and don’t hesitate to put a $20 bet on the table if the true count goes to +5 or more. As with any other blackjack game, you’re not going to be able to make a living wage if your total bankroll is $1000. If you’ve got a $5000 bankroll, you will be able to play with quarter chips, and you will have many occasions to place the max $100 bets. But be aware of any substantial negative swings, and cut back your bets accordingly.
Future of the Over/Under Side Bet
Over Under 13 Blackjack Odds Poker
Will the over/under game survive? Caesars Tahoe has been offering it on six tables now for more than a year, which indicates a better chance for longevity than most gimmick games. Caesars knows that card counters are attacking the game, and for the most part they’ve been welcoming them. This is because most card counters are using standard card counting systems to determine when to bet over and under, and such systems correlate poorly to the over/under effects of removal.
With the Hi-Lo card counting system, for example, you do not have an advantage on the over bet until your true count is +5 (as opposed to +3 with the Over/Under Count), and you do not have an advantage on the under bet until your true count is -8 (as opposed to -4 with the Over/Under). This means that with 4 ½ decks dealt out, the Hi-Low count would accurately recognize 3 ½ over/under betting opportunities per 100 hands. The Over/Under Count would recognize 13 ½ betting opportunities.
Most card counters using normal blackjack systems will bet far too often when the house has the advantage, simply because their blackjack systems are not designed to identify over/under opportunities. You cannot beat this game with a small spread and a normal blackjack card counting system.
So, despite this report, I suspect Caesars will continue to profit substantially from both card counters and non-counters at their over/under tables.
Player Advantage with Various Over/Under Betting Strategies in 6-Deck Games
| 4 Decks Dealt | 4.5 Decks Dealt | 5 Decks Dealt | |
|---|---|---|---|
| Flat Bet | -0.12% | +0.07% | +0.41% |
| 1-2 Spread | +0.22% | +0.52% | +1.01% |
| 1-4 Spread | +0.67% | +1.08% | +1.61% |
Over/Under Supplement for 1, 2, 4 and 8 deck Games
Since the initial Over/Under Report was published a few months ago, one- and two-deck over/under games have appeared in Reno. Others using various numbers of decks are reportedly being offered on cruise ships and in overseas casinos. This supplement to the Over/Under Report will aid you in beating these games with any number of decks.
Assumptions
Each page of this supplement analyzes Over/Under games with a different number of decks: 1, 2, 4, 6, and 8. At the top of each page is the number of decks in play, and the assumed rules. If you are playing in a game with a different set of rules, adjust the advantages accordingly.
For example, I’ve analyzed the 2-deck game with Reno rules. The advantage at a true count of 0 is -0.7. If you find a 2-deck Vegas Strip rules game, your advantage at 0 would be -0.3. All of the figures in the advantage column should be adjusted accordingly.
For ease of use, I have analyzed your expectation with a flat bet, a 1-2 spread, and a 1-4 spread. If you are playing in a game with a different set of rules, you may approximate your advantage simply by adding or subtracting, as appropriate, the difference in your starting advantage from the “win rates” shown.
All frequency distributions assume the Over/Under Count is being used as described in the report.
Note: These frequency distributions were obtained via computer simulation with “fixed” shuffle points, so they are not symmetrical. The simulations also used a different method of rounding than the mathematical model used for the Report. For this reason, the 6-deck distribution in the supplement is different from that in the report. You may note that the 6-deck win rates in the supplement are 0.1% to 0.2% lower than in the Report. The win rates are more accurate in the supplement.
| Count | Advantage | 65% | 75% | 85% |
|---|---|---|---|---|
| -25 | 26.6 | 0 | 0 | 0.1 |
| -24 | 21.5 | 0 | 0 | 0.1 |
| -23 | 20.4 | 0 | 0 | 0.1 |
| -22 | 19.3 | 0 | 0 | 0.1 |
| -21 | 18.2 | 0 | 0 | 0.1 |
| -20 | 17.1 | 0 | 0.1 | 0.1 |
| -19 | 16.0 | 0 | 0.1 | 0.1 |
| -18 | 14.9 | 0.1 | 0.1 | 0.1 |
| -17 | 13.8 | 0.1 | 0.2 | 0.2 |
| -16 | 12.6 | 0.1 | 0.2 | 0.3 |
| -15 | 11.5 | 0.1 | 0.3 | 0.3 |
| -14 | 10.4 | 0.1 | 0.4 | 0.5 |
| -13 | 9.3 | 0.2 | 0.3 | 0.5 |
| -12 | 8.2 | 0.4 | 0.6 | 0.7 |
| -11 | 7.1 | 0.3 | 0.4 | 0.6 |
| -10 | 6.0 | 0.8 | 1 | 1.2 |
| -9 | 4.8 | 0.8 | 1.1 | 1.5 |
| -8 | 3.7 | 1.2 | 1.3 | 1.5 |
| -7 | 2.6 | 2.3 | 2.3 | 2.5 |
| -6 | 1.5 | 2 | 2.4 | 2.1 |
| -5 | 0.4 | 3.4 | 3.4 | 3.5 |
| -4 | -0.7 | 4.7 | 4.1 | 4.6 |
| -3 | -1.5 | 5.6 | 6.5 | 6.0 |
| -2 | -1.1 | 8.3 | 7.5 | 6.5 |
| -1 | -0.8 | 7.5 | 6.6 | 5.8 |
| 0 | -0.4 | 30 | 28 | 26.8 |
| +1 | -0.1 | 6.3 | 5.6 | 4.9 |
| +2 | 0.3 | 7.1 | 6.3 | 5.6 |
| +3 | 1.1 | 4.7 | 5.7 | 5.2 |
| +4 | 2.7 | 3.6 | 3.2 | 3.8 |
| +5 | 4.2 | 3.3 | 3.3 | 3.4 |
| +6 | 5.7 | 1.6 | 2.0 | 1.8 |
| +7 | 7.2 | 1.8 | 2.1 | 2.3 |
| +8 | 8.8 | 1 | 1 | 1.2 |
| +9 | 10.3 | 0.8 | 1.1 | 1.4 |
| +10 | 11.8 | 0.6 | 0.9 | 1.1 |
| +11 | 13.3 | 0.3 | 0.3 | 0.5 |
| +12 | 14.9 | 0.3 | 0.5 | 0.6 |
| +13 | 16.4 | 0.2 | 0.3 | 0.4 |
| +14 | 17.9 | 0.1 | 0.2 | 0.4 |
| +15 | 19.4 | 0.1 | 0.1 | 0.2 |
| +16 | 21.0 | 0.1 | 0.1 | 0.3 |
| +17 | 22.5 | 0.1 | 0.1 | 0.2 |
| +18 | 24.0 | 0 | 0.1 | 0.1 |
| +19 | 25.5 | 0 | 0.1 | 0.1 |
| +20 | 27.1 | 0 | 0.1 | 0.1 |
| +21 | 28.6 | 0 | 0 | 0.1 |
| +22 | 30.1 | 0 | 0 | 0.1 |
| +23 | 31.6 | 0 | 0 | 0.1 |
| +24 | 33.2 | 0 | 0 | 0.1 |
| +25 | 34.8 | 0 | 0 | 0.1 |
| Win Rate (%) | ||||
| Flat Bet: | 1.6 | 2.2 | 3.1 | |
| 1-2 Spread: | 2.5 | 3.1 | 4.1 | |
| 1-4 Spread: | 3.2 | 3.9 | 4.9 | |
2-Deck (Reno Rules) Over/Under Count Win Rates
| Count | Advantage | 65% | 75% | 85% |
|---|---|---|---|---|
| -19 | 15.7 | 0 | 0 | 0.1 |
| -18 | 14.5 | 0 | 0 | 0.1 |
| -17 | 13.4 | 0 | 0 | 0.1 |
| -16 | 12.3 | 0 | 0.1 | 0.1 |
| -15 | 11.2 | 0 | 0.1 | 0.1 |
| -14 | 10.1 | 0 | 0.1 | 0.2 |
| -13 | 9.0 | 0.1 | 0.1 | 0.2 |
| -12 | 7.9 | 0.1 | 0.2 | 0.4 |
| -11 | 6.8 | 0.1 | 0.3 | 0.4 |
| -10 | 5.7 | 0.2 | 0.4 | 0.6 |
| -9 | 4.6 | 0.4 | 0.6 | 0.9 |
| -8 | 3.4 | 0.7 | 0.9 | 1.2 |
| -7 | 2.3 | 1.1 | 1.5 | 1.8 |
| -6 | 1.2 | 1.5 | 1.8 | 2.0 |
| -5 | 0.1 | 2.6 | 2.9 | 3.1 |
| -4 | -1.0 | 4.0 | 4.1 | 4.1 |
| -3 | -1.8 | 6.0 | 6.3 | 5.8 |
| -2 | -1.4 | 9.5 | 9.1 | 9.0 |
| -1 | -1.1 | 16.2 | 14.6 | 13 |
| 0 | -0.7 | 19.6 | 18.5 | 17.7 |
| +1 | -0.4 | 14.6 | 13.2 | 11.8 |
| +2 | 0 | 8.4 | 8.1 | 8.1 |
| +3 | 0.9 | 5.3 | 5.6 | 5.3 |
| +4 | 2.4 | 3.6 | 3.6 | 3.8 |
| +5 | 3.9 | 2.3 | 2.6 | 2.9 |
| +6 | 5.4 | 1.3 | 1.6 | 1.7 |
| +7 | 7 | 1.0 | 1.3 | 1.6 |
| +8 | 8.5 | 0.6 | 0.8 | 1 |
| +9 | 10 | 0.3 | 0.5 | 0.8 |
| +10 | 11.5 | 0.2 | 0.4 | 0.6 |
| +11 | 13 | 0.1 | 0.2 | 0.3 |
| +12 | 14.6 | 0.1 | 0.1 | 0.3 |
| +13 | 16.1 | 0.1 | 0.1 | 0.2 |
| +14 | 17.6 | 0 | 0.1 | 0.2 |
| +15 | 19.1 | 0 | 0.1 | 0.1 |
| +16 | 21.2 | 0 | 0.1 | 0.1 |
| +17 | 22.7 | 0 | 0 | 0.1 |
| +18 | 24.2 | 0 | 0 | 0.1 |
| +19 | 25.7 | 0 | 0 | 0.1 |
| Win Rate (%) | ||||
| Flat bet: | 0.5 | 0.9 | 1.5 | |
| 1-2 spread: | 1.1 | 1.6 | 2.3 | |
| 1-4 spread: | 1.7 | 2.3 | 3.1 | |
| Count | Advantage | 65% | 75% | 85% |
|---|---|---|---|---|
| -14 | 10.4 | 0 | 0 | 0.1 |
| -13 | 9.3 | 0 | 0 | 0.1 |
| -12 | 8.1 | 0 | 0.1 | 0.1 |
| -11 | 7.0 | 0 | 0.1 | 0.2 |
| -10 | 5.9 | 0.1 | 0.1 | 0.3 |
| -9 | 4.8 | 0.1 | 0.2 | 0.4 |
| -8 | 3.7 | 0.2 | 0.4 | 0.6 |
| -7 | 2.6 | 0.4 | 0.7 | 1.0 |
| -6 | 1.5 | 0.7 | 1.0 | 1.4 |
| -5 | 0.3 | 1.5 | 1.8 | 2.2 |
| -4 | -0.8 | 2.8 | 3.2 | 3.5 |
| -3 | -1.5 | 5.2 | 5.4 | 5.6 |
| -2 | -1.2 | 9.5 | 9.3 | 9.0 |
| -1 | -0.8 | 18.4 | 17.2 | 16.1 |
| 0 | -0.5 | 26.6 | 23.9 | 22.4 |
| +1 | -0.1 | 16.6 | 15.8 | 14.8 |
| +2 | 0.2 | 8.5 | 8.8 | 8.2 |
| +3 | 1.1 | 4.6 | 5.1 | 5.1 |
| +4 | 2.6 | 2.5 | 3.0 | 3.3 |
| +5 | 4.1 | 1.3 | 1.6 | 2.0 |
| +6 | 5.7 | 0.5 | 1.0 | 1.3 |
| +7 | 7.2 | 0.3 | 0.6 | 0.8 |
| +8 | 8.7 | 0.1 | 0.3 | 0.5 |
| +9 | 10.2 | 0.1 | 0.2 | 0.4 |
| +10 | 11.8 | 0 | 0.1 | 0.2 |
| +11 | 13.3 | 0 | 0.1 | 0.1 |
| +12 | 14.8 | 0 | 0 | 0.1 |
| +13 | 16.3 | 0 | 0 | 0.1 |
| +14 | 17.9 | 0 | 0 | 0.1 |
| Win Rate (%) | ||||
| Flat bet: | 0 | 0.3 | 0.7 | |
| 1-2 spread: | 0.4 | 0.9 | 1.4 | |
| 1-4 spread: | 0.9 | 1.4 | 2 | |
6-Deck (Reno Rules) Over/Under Count Win Rates
| Count | Advantage | 65% | 75% | 85% |
|---|---|---|---|---|
| -12 | 8 | 0 | 0 | 0.1 |
| -11 | 6.9 | 0 | 0 | 0.1 |
| -10 | 5.8 | 0 | 0.1 | 0.1 |
| -9 | 4.7 | 0 | 0.1 | 0.2 |
| -8 | 3.6 | 0.1 | 0.1 | 0.3 |
| -7 | 2.5 | 0.1 | 0.3 | 0.6 |
| -6 | 1.4 | 0.3 | 0.6 | 0.9 |
| -5 | 0.3 | 0.8 | 1.3 | 1.7 |
| -4 | -0.9 | 1.8 | 2.4 | 2.8 |
| -3 | -1.6 | 4.2 | 4.6 | 5 |
| -2 | -1.2 | 8.8 | 8.9 | 8.9 |
| -1 | -0.9 | 18.7 | 17.9 | 17.1 |
| 0 | -0.5 | 32.1 | 29.3 | 26.6 |
| +1 | -0.2 | 17.6 | 17 | 16.1 |
| +2 | 0.2 | 8.3 | 8.4 | 8.4 |
| +3 | 1 | 4 | 4.4 | 4.6 |
| +4 | 2.6 | 1.9 | 2.1 | 2.6 |
| +5 | 4.1 | 0.8 | 1.2 | 1.6 |
| +6 | 5.6 | 0.3 | 0.7 | 0.9 |
| +7 | 7.1 | 0.1 | 0.3 | 0.6 |
| +8 | 8.7 | 0.1 | 0.1 | 0.3 |
| +9 | 10.2 | 0 | 0.1 | 0.2 |
| +10 | 11.7 | 0 | 0.1 | 0.1 |
| +11 | 13.2 | 0 | 0 | 0.1 |
| +12 | 14.8 | 0 | 0 | 0.1 |
| Win Rate (%) | ||||
| Flat bet: | -0.2 | 0 | 0.3 | |
| 1-2 spread: | 0.1 | 0.4 | 0.8 | |
| 1-4 spread: | 0.5 | 0.9 | 1.4 | |
Over Under 13 Blackjack Odds Against
| Count | Advantage | 65% | 75% | 85% |
|---|---|---|---|---|
| -11 | 7 | 0 | 0 | 0.1 |
| -10 | 5.9 | 0 | 0 | 0.1 |
| -9 | 4.8 | 0 | 0 | 0.1 |
| -8 | 3.7 | 0 | 0.1 | 0.2 |
| -7 | 2.6 | 0.1 | 0.2 | 0.4 |
| -6 | 1.4 | 0.2 | 0.4 | 0.7 |
| -5 | 0.4 | 0.4 | 0.9 | 1.3 |
| -4 | -0.8 | 1.3 | 1.8 | 2.5 |
| -3 | -1.5 | 3.3 | 3.9 | 4.4 |
| -2 | -1.2 | 8.1 | 8.5 | 8.5 |
| -1 | -0.8 | 19.6 | 18.4 | 17.4 |
| 0 | -0.5 | 36 | 33.1 | 30 |
| +1 | -0.1 | 18.4 | 17.6 | 16.8 |
| +2 | 0.3 | 7.6 | 8.1 | 8.1 |
| +3 | 1.1 | 3 | 3.7 | 4.2 |
| +4 | 2.7 | 1.2 | 1.8 | 2.3 |
| +5 | 4.2 | 0.5 | 0.8 | 1.3 |
| +6 | 5.7 | 0.2 | 0.4 | 0.7 |
| +7 | 7.2 | 0.1 | 0.2 | 0.4 |
| +8 | 8.7 | 0 | 0.1 | 0.2 |
| +9 | 10.3 | 0 | 0 | 0.1 |
| +10 | 11.8 | 0 | 0 | 0.1 |
| +11 | 13.3 | 0 | 0 | 0.1 |
| Win Rate (%) | ||||
| Flat bet: | -0.3 | -0.1 | 0.2 | |
| 1-2 spread: | 0 | 0.2 | 0.6 | |
| 1-4 spread: | 0.3 | 0.6 | 1.2 | |
Over Under 13 Blackjack Odds Explained
For the Unbalanced Over/Under Count and more information on professional blackjack card counting systems, see the Blackjack Forum Professional Gambling Library. ♠
Back to Arnold Snyder's Blackjack Forum Online Home